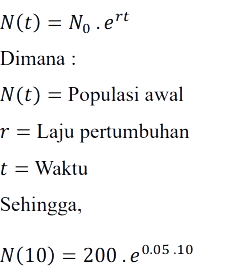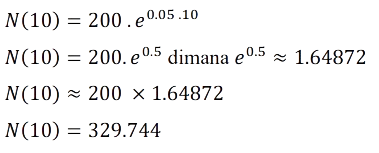Pemodelan matematika merupakan suatu proses representasi fenomena dunia nyata dalam bentuk model matematika untuk memahami, menganalisis, dan memprediksi berbagai aspek dari fenomena tersebut. Model matematika ini bisa berupa persamaan, fungsi, grafik, atau bentuk matematika lainnya yang membantu dalam menggambarkan hubungan antar variabel dalam fenomena yang dipelajari.
Dalam hal ini, akan dibahas suatu bentuk model matematika yaitu Model Pertumbuhan Eksponensial. Apa yang telah kamu ketahui mengenai bentuk dari model matematika ini?
Pernahkah kamu melihat soal berupa proses pembelahan planaria? ya, itu salah satu contoh dari pertumbuhan eksponensial.
Mari membahas mengenai apa itu Pertumbuhan Eksponensial!
Model Pertumbuhan Eksponensial
Model Pertumbuhan Eksponensial merupakan model yang menggambarkan bagaimana suatu jumlah dapat berubah secara proporsional terhadap ukuran saat ini. Hal ini berarti bahwa laju perubahan sebanding dengan ukuran saat ini.
Dalam model pertumbuhan eksponensial, pertumbuhan atau penurunan terjadi dengan laju yang konstan, tetapi karena jumlah yang ada terus berubah, laju perubahan absolut (jumlah perubahan) juga berubah. Jika laju pertumbuhan positif, jumlah atau populasi akan bertambah secara eksponensial. Jika laju pertumbuhan negatif, jumlah atau populasi akan berkurang secara eksponensial.
Model pertumbuhan eksponensial :
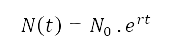
Dengan unsur - unsur sebagai berikut :
Permasalahan :
Populasi awal dari bakteri adalah 200 dengan laju pertumbuhan bakteri tersebut adalah 0.05 per jam. Berapa jumlah bakteri yang ada setelah 10 jam?
Penyelesaian :
Permasalahan di atas, akan diselesaikan secara analitik dan numerik.
- Analitik
-
Model Matematika
-
Penyelesaian Analitik
-
Kesimpulan
jadi, secara analitik dalam waktu 10 jam diperoleh 329 Bakteri.
- Numerik
Akan dicari penyelesaian numerik dengan menggunakan metode Euler.
Bentuk dasar dari metode Euler adalah
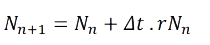
Dimana :
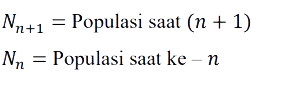
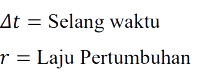
Sehingga
Jadi, dengan metode Euler setelah 10 jam diperoleh jumlah bakteri sebanyak 325 bakteri.
Kesimpulan
Dari permasalahan mengenai pertumbuhan pada sejumlah bakteri setelah waktu tertentu, diperoleh jumlah bakteri setelah 10 jam dengan metode analitik dan numerik. Dengan Analitik diperoleh jumlah bakteri setelah 10 jam adalah 329 bakteri, sedangkan secara numerik yang dihitung dengan metode Euler diperoleh jumlah bakteri setelah 10 jam adalah 325 bakteri. Dari hasil tersebut diperoleh bahwa tidak ada perbedaan besar pada jumlah bakteri setelah 10 jam baik secara analitik maupun numerik.